potentials-type-4 | Scymol project

Type 4 forces

**Figure 1.** This force category includes forces that result from the angular strain generated by three consecutively bonded atoms i, j, and k.

The total energy $E_{Type\ \ 4}$ of the system at any given time is given by the summation of the energies present at each angle ($\theta_{i,j,k}$) formed by atoms i, j, and k (see Figure 1). $$E_{Type\ 4}=\sum_{i,j,k}^{Bonded\ triples}E_{i,j,k},$$ where $E_{i,j,k}$ is the energy resulting from the formation of an angular strain between three bonded atoms i-j-k.

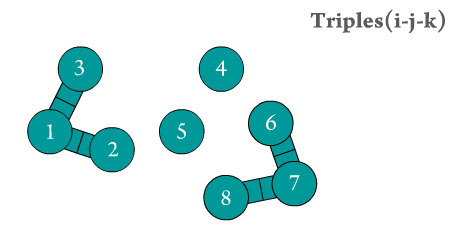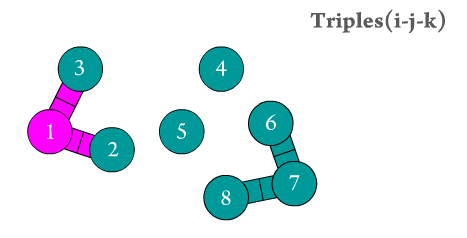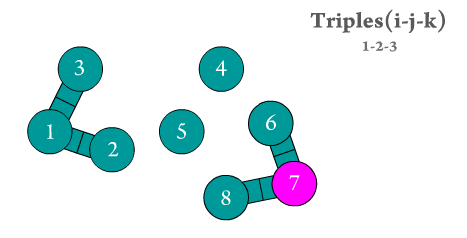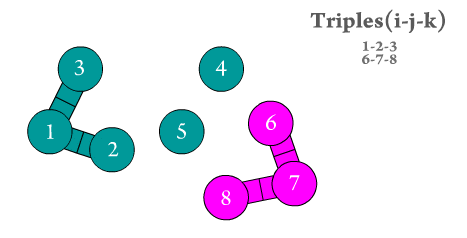
**Figure 2.** The angular *triples* are generated by Scymol by searching for every 'middle' particle bonded to two different atoms. Notice how atoms that do not form an atomic triple (three consecutively bonded atoms) are omitted.

Even though the calculation of the resulting forces (and thus, the resulting particle positions) due to the presence of angular strains is considerably harder than in type 2 interactions, the number of atomic triples usually grows with ($N$) (see Figure 2). This means that estimating angular strain effects on MD systems is computationally inexpensive.

Angular potentials often rely on applying an angular strain on particles i, j, and k if the angle formed ($\theta_{i,j,k}$) is not very close to some reference angle ($\theta_{0}$). Even though it is less common, some angular potentials may have multiple ($m$) reference (or equilibrium) angles ($\theta_{0,m}$). If the potential has several equilibrium angles, it is said that the potential has a multiplicity equal to $m$. In that case, the energy of the system is given by: $$E_{Type\ 4}=\sum_{1}^{m}\sum_{i}^{bonded\ triples}E_{(i,j,k),\ \ \ m},$$ where $E_{i,j,k}$ is the energy resulting from the formation of an angular strain between three bonded atoms i-j-k and $m$ is the multiplicity of the potential.

Example 1.
In the following example, we convert an energy potential ($E$) into its force form and we explain how the solver calculates the new particle position from this force. A common potential used in chemical systems for this force category is the Harmonic potential with multiplicity $m = 1$. The Harmonic potential is given by: $$ E_{i,j, k}=\sum_{i}^{N}{a_{i,j,k}\times\left(\theta_{i,j,k}-\theta_0\right)^2} $$

Notice how the magnitude of the strain (or force) depends entirely on how close the angle formed by the particles ($\theta_{i,j,k}$) and the reference angle($\theta_{0,m}$) are.

Here we show how the position of a particle i is updated by Scymol's solver using the Harmonic potential (Refer to Figure 1). Note that not all the particles are affected in similar ways; the formulae used for particle i are very different from those used for particles j and k. $$\frac{\partial E_A}{x_i}=\frac{\partial E_A}{\partial\theta_{ijk}}\ \frac{\partial\theta_{ijk}}{\partial a_1}\ \frac{\partial a_1}{\partial x_i}$$ knowing that: $$a_1=x_i-x_j,\ b_1=y_i-y_j,\ c_1=z_i-z_j$$ $$a_2=x_k-x_j,\ b_2=y_k-y_j,\ c_2=z_k-z_j$$ $$\theta_{ijk}=\cos^{-1}{\left(\frac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{a_1^2+b_1^2+c_1^2}\sqrt{a_2^2+b_2^2+c_2^2}}\right)}$$ Using SymPy's differentiation function scympy.diff(str_energy_expression), the resulting force acting on atom i in the x-coordinate is:

$$F_{i,x} = \frac{-2k \left(\theta-\theta_o\right) \left(-a_1 {\left({a_1}^2+{b_1}^2+{c_1}^2\right)}^{-1.5} {\left({a_2}^2+{b_2}^2+{c_2}^2\right)}^{-0.5} \left(a_1 a_2+b_1 b_2+c_1 c_2\right)+a_2 {\left({a_1}^2+{b_1}^2+{c_1}^2\right)}^{-0.5} {\left({a_2}^2+{b_2}^2+{c_2}^2\right)}^{-0.5}\right)}{\sqrt{-\left({\left({a_1}^2+{b_1}^2+{c_1}^2\right)}^{-1}\right) {\left({a_2}^2+{b_2}^2+{c_2}^2\right)}^{-1} {\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}^2+1}}$$

Some parts of this expression are constant and they are embedded into Scymol's source code in a more efficient way (e.g., grouping exponents and terms) for faster calculations.

4/5